NEW DEMO

Here we want to develop algebraic steps to determine polynomial interpolation for two groups of 4 dots that share a dot. The groups are labeled in the figure below and they share the dot 15. The goal is to determine \(\Large p_{1}(x)\) the interpolant for the first group and \(\Large p_{2}(x)\) is the interpolant for the second group.

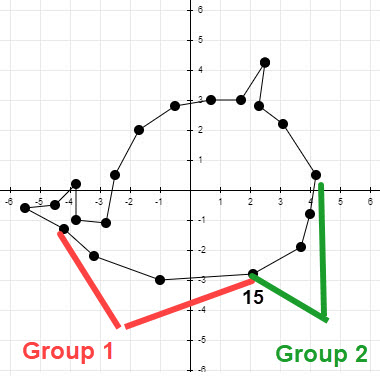
The coordinates of the first group are respectively \[\large {(x, y): (-4.2, -1.3), (-3.2, -2.2), (-1, -3), (2.1, -2.8)}\] The coordinates of the second group are respectively \[\large {(x, y): (2.1, -2.8), (3.7, -1.9), (4.0, -0.8), (4.2, 0.5)}\] Each of these polynomials will be a smooth graph with \(\Large p_{1}(x)\) over interval [-4.2, 2.1] while \(\Large p_{2}(x)\) is over interval [2.1, 4.2].

The form of polynomial \(\Large p_{1}(x)\) is \[\Large p_{1}(x)= a_{3} x^{3} + a_{2} x^{2} + a_{1} x + a_0 \] for each of the members of the first group substitute the the x-coordinate into the equation for x and then set \(\Large p_{1}(x)\) equal to the corresponding y-coordinate. This gives us the following four equations.

\[\Large -1.3 = a_{3} (-4.2)^{3} + a_{2} (-4.2)^{2} + a_{1} (-4.2) + a_0 = -74.088 a_{3} + 17.64 a_{2} - 4.2 a_{1} + a_0 \] \[\Large -2.2= a_{3} (-3.2)^{3} + a_{2} (-3.2)^{2} + a_{1} (-3.2) + a_0 = -32.768 a_{3} + 10.24 a_{2} - 3.2 a_{1} + a_0 \] \[\Large -3 = a_{3} (-1)^{3} + a_{2} (-1)^{2} + a_{1} (-1) + a_0 = a_0 = -1 a_{3} + 1 a_{2} - 1 a_{1} + a_0 \] \[\Large -2.8 = a_{3} (2.1)^{3} + a_{2} (2.1)^{2} + a_{1} (2.1) + a_0 = 9.26 a_{3} + 4.41 a_{2} + 2.1a_{1} + a_0 \] Simpler expressions are given by the equations \[\Large -1.3 = -74.088 a_{3} + 17.64 a_{2} - 4.2 a_{1} + a_0 \] \[\Large -2.2= -32.768 a_{3} + 10.24 a_{2} - 3.2 a_{1} + a_0 \] \[\Large -3 = -1 a_{3} + 1 a_{2} - 1 a_{1} + a_0 \] \[\Large -2.8 = 9.26 a_{3} + 4.41 a_{2} + 2.1a_{1} + a_0 \]

To solve for the coefficients \[\Large a_{3}, a_{2}, a_{1}, a_0 \] we have several choices. One is to use successive algerbraic substitutions to get long equations that boil down to compute each coefficient one at a time. This procedure it is quite error prone. (Math to the rescue!) A much better alternative is use linear algebra and matrices to determine the coefficients. $$ M = \begin{bmatrix} -74.088&17.64&-4.2&1\\ -32.768&10.24&-3.2&1\\ -1&1&-1&1\\ 9.26&4.41&2.1&1\\ \end{bmatrix} c = \begin{bmatrix} a_{3}\\ a_{2}\\ a_{1}\\ a_0 \\ \end{bmatrix} rh = \begin{bmatrix} -1.3\\-2.2\\-3\\-2.8\\ \end{bmatrix} $$ The matrix M is called the coefficient matrix, c is called matrix of unknowns, and rh is called the right hand side of the matrix equation \(\large M \times c = rh\). To solve for c more linear algebra is needed and we omit this part. (Take a course in linear algebra, which is one of the main sources for solving a variety of problems.) The solution of the matrix equation is $$ c = \begin{bmatrix} - 0.013783 \\ 0.05184 \\ 0.053112\\ - 3.0125 \\ \end{bmatrix} $$ Thus the polynomial of the first group is \[\Large p_{1}(x)= - 0.013783 x^{3} + 0.05184 x^{2} + 0.053112 x - 3.0125 \]

The polynomial for the second group can be computed in a similar way and the result is \[\Large p_{2}(x)= 1.9361 x^{3} - 17.3728 x^{2} + 51.3006 x - 51.9474\]

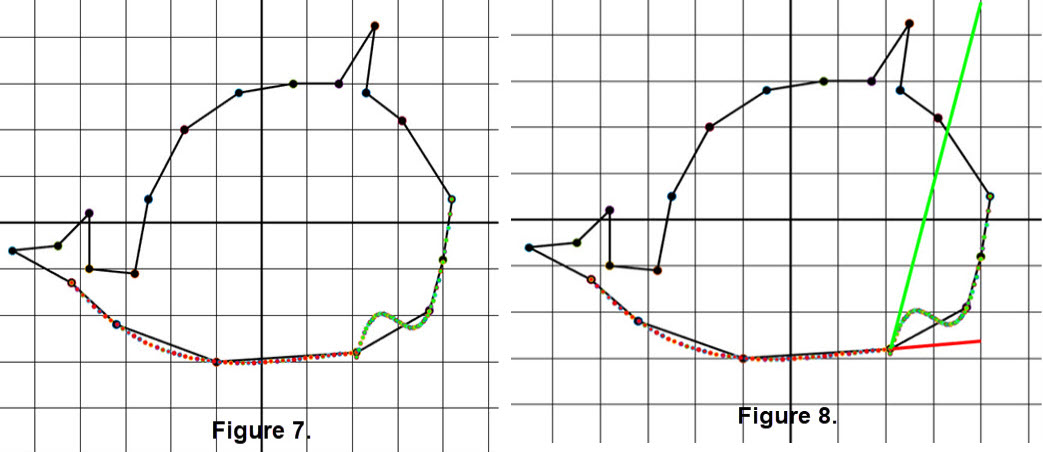
Then, using a bit of calculus we can check the slope at the left of dot 15 and at the right of dot 15 because we have the two polynomials. Differentiate each polynomial and evaluate the derivatives at x = 2.1. At dot 15 at the left the slope is m = 0.0887, while on the right the slope is m = 3.9494. The result is that we have a sharp point at dot 15. Below, see Figure 7 for the graphs of the polynomials and Figure 8 shows the slopes at dot 15. (These figures were enlarged a little to emphasize the polynomials and slopes.)